Hydrodynamic Approach to B-O on the Double

Exploiting analyticity condition pertaining to B-O on the double, if we describe the following:

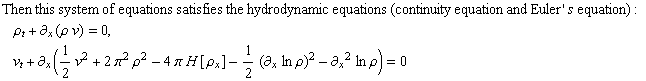
    Essentially, then, we have that every solution of B-O on the Double (soliton as well as arbitrary non-soliton solutions)correspond to some description of the hydrodynamic system, and vice-versa.
    It is proven that Classical Sutherland Model which describes the interaction of an N-body system with 1/r^2 interaction, in the limit of N going to infinity, turns into continuous hydrodynamic system.
    We verified this, by taking the actual 1-Soliton Solution of the hydrodynamic system, approximated it with a finite-body Sutherland system, and plotted the evolution of position of the particles, which verified that they travel with a permanent form, just like a Soliton.
    The following are the density and velocity functions corresponding to 1-soliton solution in the hydrodynamic representation:

ρ1per[x, t] := 1/(2π) (Sinh[b]/(Cosh[b] + Cos[x - vt]) +    Sinh[b]/(Cosh[a] - Cosh[b])) ;

v1per[x, t] := V + Sinh[a]/(Cosh[a] + Cos[x - vt]) - Sinh[a]/(Cosh[a] - Cosh[b]) ;

Translating it to the Sutherland Model of 100 particles,the initial profile looks like the following:

[Graphics:HTMLFiles/index_6.gif]

And it evolves like the following:

Indeed,a Soliton Profile!

Created by Mathematica  (April 26, 2006) Valid XHTML 1.1!